hdu1395

maksyuki 发表于 oj 分类，标签: ,
15 9月 2015
0

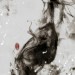
2^x mod n = 1

Problem Description

Give a number n, find the minimum x(x>0) that satisfies 2^x mod n = 1.

Input

One positive integer on each line, the value of n.

Output

If the minimum x exists, print a line with 2^x mod n = 1.

Print 2^? mod n = 1 otherwise.

You should replace x and n with specific numbers.

Sample Input

2

5

Sample Output

2^? mod 2 = 1

2^4 mod 5 = 1

Author

MA, Xiao

Source

ZOJ Monthly, February 2003

 

题目类型：欧拉定理+暴力枚举

算法分析：直接排除n为1和偶数的情况，此时一定无解。若n为大于1的奇数，则使用欧拉定理得出合理的解m，最后枚举1~tt中所有的指数，对于每个指数使用快速幂判断是否余数为1，更新最小值，当然更好的方法是枚举n的所有因子，直接判断因子是否满足条件。这道题的数据比较水，所以暴力也可过~~